Say that your job is to write a filter program which takes in a block of text and either accepts or rejects the block of text based on whether the text has expletives, such as on Neopets. Your block of text is n characters long and you have a finite set of expletives of m total characters.
How would you go about solving this?
The naive way, obviously, is to split the text into words and for each word, check it against every expletive to see if it matches or not. In the worst case, when there are no expletives in the text, the runtime of your filter will be O(n*m) because you will end up checking every single character of the text against your set of words.
I'm going to explain how you can use the Aho-Corasick string matching algorithm to solve this problem much faster, in O(n+m). If you want to know exactly which expletives were contained in the text and what index they were found, then your runtime will be O(n+m+z) where z is the number of expletives (I'll call it 'keyword' or 'pattern' from here on) you matched.
This algorithm is especially useful if your set of patterns is large and does not change often. We will cover the method which returns the particular matched patterns, since we can always simplify the algorithm to solve our filter problem.
Here is a rundown of how it works: the algorithm first takes the m keywords to build a trie data structure. We construct a special way to traverse this trie. Then the algorithm processes the text sequentially so once it processes a character at an index, it will not processes at this index again. As the text is being processed, as soon as any one of the patterns is matched, it will output the pattern matched. If you have another text to process, just go ahead and run the algorithm again, but don't reconstruct your trie if your set of patterns doesn't change.
Let's go through an example where the trie is already constructed, and shamelessly, let's use the example on Wikipedia, since that one is good, but I will explain it further.
Here the text string is: 'abccab' and our dictionary is {'a', 'ab', 'bc', 'bca', 'c', 'caa'}. We will keep a string called our 'matched string' which denotes a what we have read from the text string but not truncated yet. It is a string which is a prefix of any word in the dictionary. Ignore the coloured lines in the image.
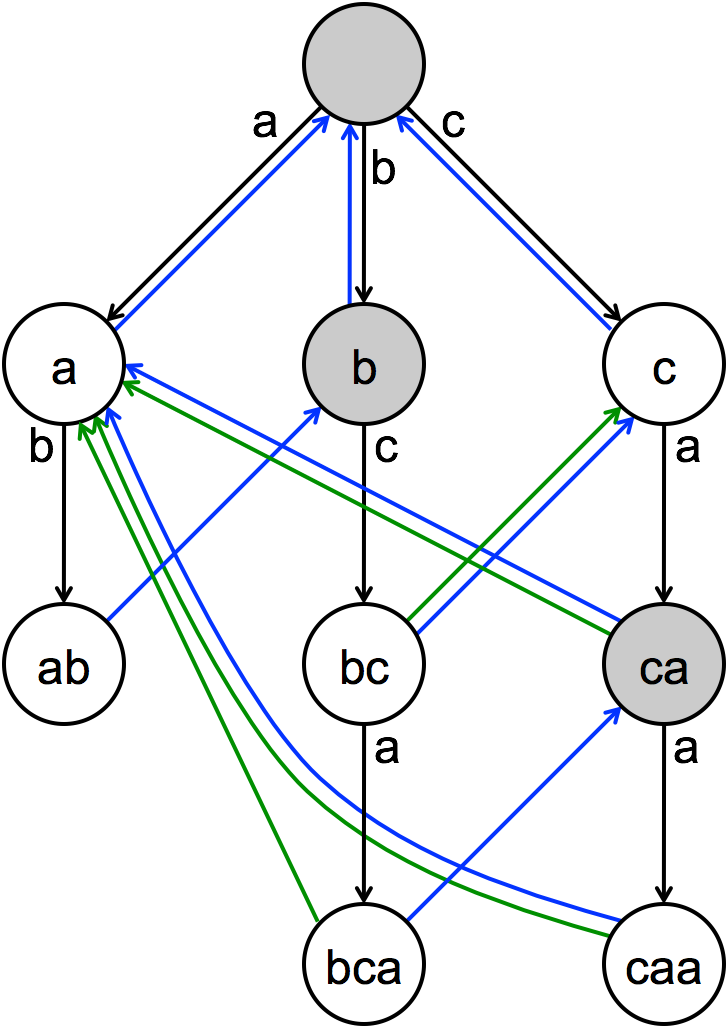
First we process 'a' from 'abccab'. 'a' is a word, so we output it. Then we process the next character 'b'. So far our matched string is 'ab', which is a word, so output it. Next we get 'abc', which is not a word. In this case, we find the next largest suffix of 'ab' (forgetting about the c temporarily) present in the graph which descends immediately from the root, which is 'b'. 'b' is not a word, so don't output it. Then we try to append 'c' again to our matched string, giving us 'bc'. 'bc' is a word, so output it. Read in the next character: 'bcc' is not a word, so we find the largest suffix of 'bc' which starts from the root, which is 'c'. 'c' is a word, so output it. Try the 'c' again, to get 'cc'. 'cc' is not a word, so we get the largest suffix of 'cc', which is 'c', a word, and output it again. 'ca' is not a word, and the largest suffix is 'a', output that. 'ab' is a word, so output that.
Notice that whenever we try to append a letter and as a result, our matched string is not a prefix, we have to move to a different node which marks the end of the next largest suffix before we can append the letter again. The transition from our current node to the node of the next largest suffix is called a 'failure transition' from our current node to its fail state node. For example, when 'abc' doesn't match, the fail state of 'ab' is the 'b' which descends from the root.
This way of assigning failure states is the special feature of the Aho-Corasick algorithm which allows the text to be processed in one pass: we keep updating our matched string, outputting a word and index whenever the matched string matches one of the words in the dictionary. When our matched string is no longer a prefix of any word in the dictionary, we truncate the matched string from the front until it is, and keep reading in more characters from the text input. At the termination of the Aho-Corasick algorithm, we will have outputted all keywords present and their respective indices.
Ignoring the construction of how to get these failure transitions, you can see that the runtime to construct the trie is O(m) and to process the text is O(n) since we do a single pass through the text, and we can truncate at most n characters. We'll cover how to get these failure transitions next time, but note that this will happen in O(n). Outputting occurs in O(z) though note that in the example 'aaaa' with dictionary {'a', 'aa', 'aaa', 'aaaa'} we will have 10 outputs since every single occurrence is found.
I hope my discussion has given you a basic intuition on how Aho-Corasick works. I will be posting a discussion on its implementation in Python soon. If you have any questions or would like to point out an error or other comment, send me a message or leave a message below. Don't worry, I don't filter your comments. :)