Here is just a short explanation about tries, which I will come back and add to if I have time/find it necessary. A trie is a tree graph used to store a dictionary of words. It is much faster than set (assuming binary search tree implementation) because 1) inserting a string of length L into set will take O(L*logk) for k words in the set whereas inserting into a trie takes O(L) and 2) the same goes for searching.

Say we want to put {kimbap, kimberley, apple, app, jello} into a trie. Our trie will look like this:

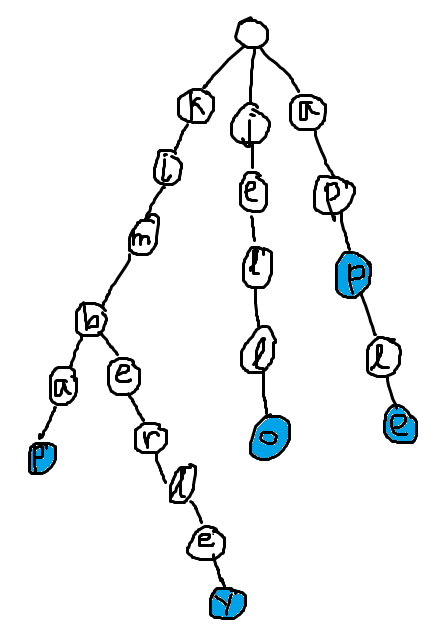
The root contains no character, and every other node is a letter of the keyword. The blue nodes mark the end of a word in the dictionary. You can see that to insert one word, you traverse down the tree L times to insert characters that are not already there. If I wanted to insert 'kim', I would not insert any new nodes. I would get to k from the root, go down to i, which I can get to from k, then go down to m and mark the presence of a completed word at 'm'. Note that words MUST begin one level below the root, and cannot start in the middle of the graph.